Q2
( a )
Use Taylor's theorem to evaluate √10 correct to four significant figures.
5
( b )
Evaluate:
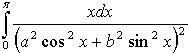
5
( c )
Determine the asymptotes of 4x3 - 3xy2 - y3 + 2x2 - xy - y2 - 1 = 0
5
WELCOME TO IP UNIVERSITY QUESTION PAPERS WEBSITE
Through this website, an attempt is being made to
provide all the previous year question papers on-line.
Currently
work is underway only for the B.Tech. Stream question papers.
About
Guru Gobind Singh Indraprstha University (GGSIPU)
Back to Homepage( ippapers.tripod.com )
|
(Please write your Roll No. immediately) |
Roll No. .................................. |
First Semester [B.Tech] – December 2003
|
Paper Code : ETMA – 101 Subject : Applied Mathematics - I |
|
Time : 3 Hours |
Maximum Marks : 75 |
|
Note : Attempt any 5 questions in all. At least two questions from each section. All questions carry equal marks. |
SECTION-A
|
Q1 |
( a ) |
State and prove Lagrange's Mean value theorem and verify it for the function f(x) = sin x + cos x in [0,π/2]. |
5 |
|
( b ) |
If y = (sin-1 x)2, prove that (1 –
x2) y2 - xy1 = 2 and also show
that |
5 |
|
|
( c ) |
If ρ1
and ρ2 are the
radii of curvature at the extremities of two conjugate diameters
of the ellipse |
5 |
|
Q2 |
( a ) |
Use Taylor's theorem to evaluate √10 correct to four significant figures. |
5 |
|
( b ) |
Evaluate:
|
5 |
|
|
( c ) |
Determine the asymptotes of 4x3 - 3xy2 - y3 + 2x2 - xy - y2 - 1 = 0 |
5 |
|
Q3 |
( a ) |
Show that
|
5 |
||||||||||
|
( b ) |
Test for the convergence of the following series : -
|
5 |
|||||||||||
|
( c ) |
The velocity v(km/min) of a moped, which starts from rest is given at fixed intervals of time. Estimate approximately the distance covered in 20 minutes by applying Simpson's 1/3 rule. |
5 |
|||||||||||
|
|
t |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
v |
10 |
18 |
25 |
29 |
32 |
20 |
11 |
5 |
2 |
0 |
|
|
|
Q4 |
( a ) |
Determine the length of the loop of the curve 9y2 = (x-3)(x-6)2 |
5 |
|
( b ) |
Find the area common to the cardiode r = a(1+cos θ) and the circle r = (3/2)a and also the area of the remainder of the cardiode. |
5 |
|
|
( c ) |
If the curve r = a+b cos θ (a>b) revolves about the initial line, show that the volume generated is (4/3) π a (a2 +b2 ) |
5 |
SECTION-B
|
Q5 |
( a ) |
If v = (x2 +y2 +z2 )-1/2 show that
|
5 |
|
( b ) |
If
(ii)
|
5 |
|
|
( c ) |
Expand sin(xy) in powers of (x-1) and (y-π/2) up to and including second degree terms. |
5 |
|
Q6 |
( a ) |
Find the volume of the tetrahedron bounded by the coordinate planes and the plane x + y + z = 1 |
5 |
|
( b ) |
Sketch the region of integration and evaluate:
|
5 |
|
|
( c ) |
Changing into polar coordinates and hence evaluate:
|
5 |
|
Q7 |
( a ) |
Solve:
|
5 |
|
( b ) |
Solve : ( 2xy cos x2 – 2xy +1 )dx + ( sin2 - x2 )dy = 0 |
5 |
|
|
( c ) |
Solve :
|
5 |
|
Q8 |
( a ) |
If u1=(x2 x3)/x1 , u2=(x1 x3)/x2 , u3=(x1 x2)/x3 , then evaluate J ( u1, u2, u3). |
5 |
|
( b ) |
Solve :
|
5 |
|
|
( c ) |
Solve :
|
5 |